將λ/2諧振器進行各種變形可以減小超導微帶濾波器的有效尺寸，幾種常見的半波長諧振器結構如圖4所示。

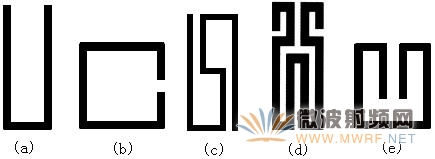
圖4 幾種常用的半波長諧振器

在圖4中，（a）為標準發夾型半波長諧振器，（b）是半波長開環諧振器，（c）、（d）、（e）為發夾型諧振器的幾種變形結構，均可用于濾波器的小型化設計。

2.5、超導濾波器制作工藝精度引起的問題

超導濾波器的濾波特性主要由導帶寬度w、導帶長度l、基片厚度h和介電常數εr等參數決定。超導濾波器制作過程中所涉及到的光刻精度，腐蝕程度，介質基片的一致性都會對濾波器濾波特性產生影響。通常采取靈敏度分析法，估算出給定加工誤差條件下微帶線傳輸特性的最壞情況，以此分析器件的性能。

3、二端口網絡理論

網絡理論是一種非常普遍的處理問題的方法，它把系統用一個由若干端口對外的未知網絡表示。微波網絡理論是微波工程強有力的工具，主要研究微波網絡各端口的物理量之間的關系，實際的微波/射頻濾波器也是用網絡分析儀進行測量。微波網絡分為線性與非線性，有源與無源，有耗與無耗，互易與非互易。

雙口元件是在微波工程中應用最多的一種元件，主要有濾波器、移相器、衰減器等。與單口元件相似，雙口元件一般采用網絡理論進行分析，但是，值得指出的是元件的網絡參數本身還是需要用場論方法求得，或者實際測量得到，從這個意義上講，場論是問題的內部本質，而網絡則是問題的外部特性。

幾乎所有的微波元件都可以由一個網絡來代替，并且可以用網絡端口參考面上的變量來描述其特性（在傳輸線上端口所在的位置，與能流方向垂直的橫截面通常稱為“參考面”）。選擇參考面的原則是在該參考面以外的傳輸線上只傳輸主模。

微波網絡有不同的網絡參量：阻抗參量Z、導納參量Y和A參量反映的是參考面上電壓與電流的關系；散射參量S、傳輸參量T反映的是參考面上歸一化入射波電壓和歸一化反射波電壓之間的關系。在微波頻率下，阻抗參量Z、導納參量Y和A參量不能直接測量，所以引入散射參量S和傳輸參量T。利用S參數，射頻電路設計者可以在避開不現實的終端條件以及避免造成待測器件損壞的前提下，用兩端口網絡的分析方法來確定幾乎所有射頻器件的特征，故S參量是微波網絡中應用最多的一種主要參量。

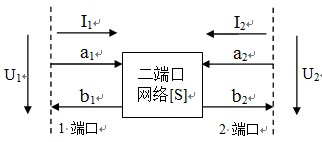
圖5 二端口網絡示意圖

S參量是根據某端口上接匹配負載的情況下所得到的歸一化波來定義的。設a_n表示第n個端口的歸一化入射波電壓，b_n表示第n個端口的反射波歸一化電壓。

所謂歸一化波，就是各端口的波用其對應端口的參考阻抗進行歸一化后得到的波，它們與同端口的電壓的關系為
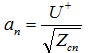（21a）

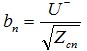(21b)

對于線性二端口網絡（如圖5所示），歸一化入射波a和反射波b之間存在如下關系

b₁=S₁₁a₁+S₁₂a₂ (22a)

b₂=S₂₁a₁+S₂₂a₂ (22b)

式（22）寫成矩陣形式為

b=Sa （23）

矩陣S稱為二端口網絡的散射矩陣或S矩陣，表示為
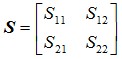(24)

式（24）中的矩陣元素稱為網絡的散射參量，各項矩陣參量的物理意義為：
S₁₁=b₁/a₁/|_a2=0表示端口2匹配時，端口1的反射系數；

S₂₂=b₂/a₂/|_a1=0表示端口1匹配時，端口2的反射系數；

S₁₂=b₁/a₂/|_a1=0表示端口1匹配時，端口2到端口1的傳輸系數；

S₂₁=b₂/a₁/|_a2=0表示端口2匹配時，端口1到端口2的傳輸系數；

a_i=0表示第i個端口接匹配負載，該端口不存在反射波。

有一點非常重要，就是所有的參量都是在對應負載匹配的情況下定義的，如果對應的負載不匹配，那么相應的反射系數和傳輸系數就不再等于S參量。

二端口網絡有幾個重要的特性參量，它們與散射參量也有著密切的關系。