卡爾曼濾波實質上就是基于觀測值以及估計值二者的數據對真實值進行估計的過程。預測步驟如圖1所示:
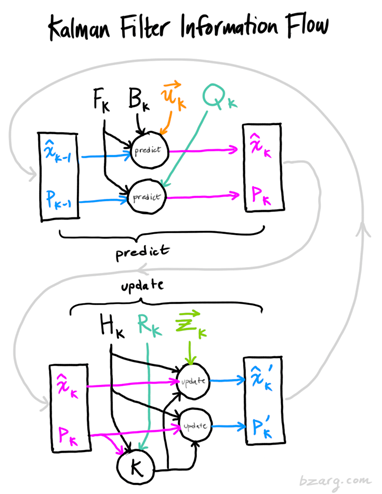
?圖1 卡爾曼濾波原理流程圖
假設我們能夠得到被測物體的位置和速度的測量值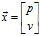 ,在已知上一時刻的最優估計值
,在已知上一時刻的最優估計值 以及它的協方差矩陣
以及它的協方差矩陣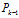 ?的條件下(初始值可以隨意取,但協方差矩陣應為非0矩陣),則有
?的條件下(初始值可以隨意取,但協方差矩陣應為非0矩陣),則有
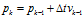
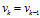
即: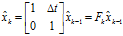 (1)
(1)
而此時,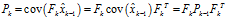 (2)
(2)
?如果我們加入額外的控制量,比如加速度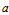 ,此時
,此時
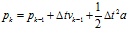
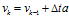
?則此時:
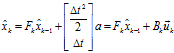 (3)
(3)
?同時,我們認為我們對系統的估計值并非完全準確,比如運動物體會突然打滑之類的,即存在一個協方差為 的噪聲干擾。因此,我們需要對
的噪聲干擾。因此,我們需要對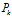 ?加上系統噪聲
?加上系統噪聲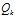 來保證描述的完備性。綜上,預測步驟的表達如下所示:
來保證描述的完備性。綜上,預測步驟的表達如下所示:
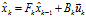 (4)
(4)
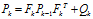 (5)
(5)
?由于誤差累積的作用,單純對系統進行估計會導致估計值越來越離譜,因此我們以傳感器的觀測數據對我們的估計進行修正。我們可以用與預測步驟類似的方法將估計值空間映射至觀測值空間,如下式所示:
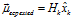 (6)
(6)
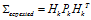 (7)
(7)
?我們假設觀測值為 。同時由于觀測數據同樣會存在噪聲干擾問題,比如傳感器噪聲等,我們將這種噪聲的分布用協方差
。同時由于觀測數據同樣會存在噪聲干擾問題,比如傳感器噪聲等,我們將這種噪聲的分布用協方差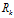 表示。此時,觀測值
表示。此時,觀測值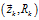 與估計值
與估計值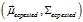 處于相同的狀態空間,但具有不同的概率分布,如圖2所示:
處于相同的狀態空間,但具有不同的概率分布,如圖2所示:
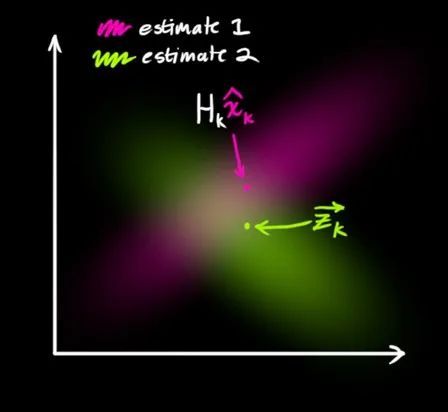
?圖2 估計值與觀測值概率分布示意圖
我們可以認為,這兩個概率分布的重疊部分,會更加趨近系統的真實數據,即有更高的置信度,比如我們估計汽車速度是5~10km/h,傳感器反饋的速度是8~12km/h,那我們有理由認為汽車的實際速度更趨近于8~10km/h這個區間。
這里將觀測值與估計值兩個分布的高斯分布相乘,其結果的高斯分布描述如下:
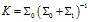 (8)
(8)
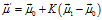 (9)
(9)
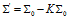 (10)
(10)
?式中:
 描述高斯分布的協方差,
描述高斯分布的協方差,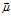 表示高斯分布的均值,矩陣
表示高斯分布的均值,矩陣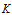 稱為卡爾曼增益矩陣。
稱為卡爾曼增益矩陣。
那么,將估計值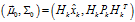 以及觀測值
以及觀測值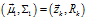 代入式(8)至式(10),可以得到:
代入式(8)至式(10),可以得到:
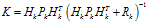 (11)
(11)
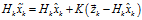 (12)
(12)
?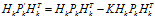 (13)
(13)
?式中,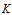 稱為卡爾曼增益。
稱為卡爾曼增益。
將式(11)至式(13)中約去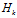 ,并化簡可得:
,并化簡可得:
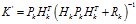 ?(14)
?(14)
 (15)
(15)
? (16)
(16)
? 即為我們所得到的最優估計值,同時
即為我們所得到的最優估計值,同時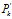 為其對應的協方差矩陣。在實際應用中,只需要使用式(4)、式(5)以及式(14)至式(16)這5個方程即可實現完整的卡爾曼濾波過程。
為其對應的協方差矩陣。在實際應用中,只需要使用式(4)、式(5)以及式(14)至式(16)這5個方程即可實現完整的卡爾曼濾波過程。
在對單一信號源濾波的場合,由于測量值與估計值具備幾乎完全相同的概率分布,為了更好的實現去噪效果,在假定被測對象變化不顯著的情況下,可以將之前(1~N)個時間節點的測量值隨機作為當前時間節點的測量值,以實現更好的去噪效果。原則上,N取值越大濾波效果越好,但也會導致濾波結果滯后越嚴重。
2. 算法實現
function output = kalmanFilter(data, Q, R, N)
if ~exist('Q', 'var')
Q = 0.01;
end
if ~exist('R', 'var')
R = 1;
end
if ~exist('N', 'var')
N = 0;
end
X = 0;
P = 1;
A = 1;
H = 1;
output = zeros(size(data));
for ii = N + 1 : length(data)
X_k = A * X;
P_k = A * P * A' + Q;
Kg = P_k * H' / (H * P_k * H' + R);
z_k = data(ii - round(rand() * N));
X = X_k + Kg * (z_k - H * X_k);
P = (1 - Kg*H) * P_k;
output(ii) = X;
end
end
3. 算法分析
采用經典卡爾曼濾波對虛擬信號及真實信號進行濾波,結果如下圖所示:
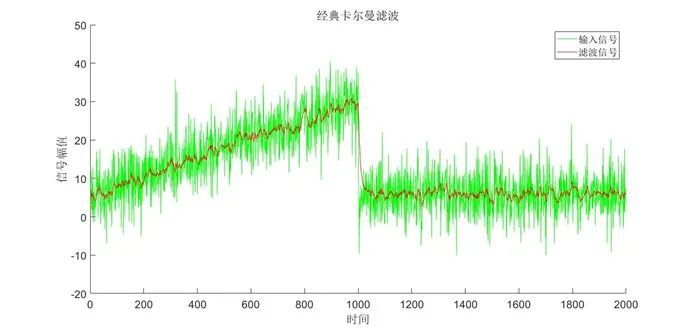
?圖3 經典卡爾曼濾波對虛擬信號濾波結果
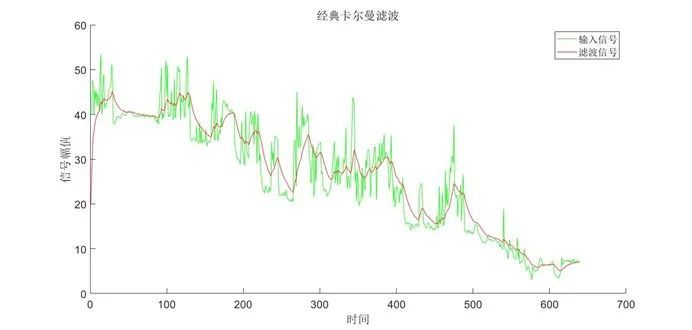
?圖4 經典卡爾曼濾波對真實信號濾波結果
從濾波結果中可以看出,經典卡爾曼對信號的濾波效果較為優秀,實時性相對較好,計算量需求極小,能夠有效去除高斯噪聲以及非高斯噪聲,基本不受脈沖信號影響。在對被測系統的建模較為精確的條件下,其性能還能夠進一步提升。其缺點主要在于需人為給定系統模型,當系統模型不精確時濾波效果會有所下降,但可以通過增加采樣頻率解決此問題。
建議應用場合:輸入信號相對平穩或已知被測系統運動學模型,同時要求運算量極小的場合。
作者:小石學CS

 粵公網安備 44030902003195號
粵公網安備 44030902003195號