簡介

精密模數轉換器應用廣泛，如儀器儀表和測量、電力線繼電保護、過程控制、電機控制等。目前，SAR 型ADC 的分辨率可達18 位甚至更高，采樣速率為數MSPS；Σ-Δ 型ADC 的分辨率則達到24 位甚至32 位，采樣速率為數百kSPS。為了充分利用高性能ADC 而不限制其能力，用戶在降低信號鏈噪聲方面（例如實現濾波器）面臨的困難越來越多。

本文討論在ADC 信號鏈中實現模擬和數字濾波器以便達到最佳性能所涉及到的設計挑戰和考慮。如圖1 所示，數據采集信號鏈可以使用模擬或數字濾波技術，或兩者的結合。精密SAR 型和Σ-Δ 型ADC 一般在第一奈奎斯特區進行采樣，因此，本文將著重討論低通濾波器。本文的意圖不是討論低通濾波器的具體設計技術，而是討論其在ADC 電路中的應用。

圖1.一般數據采集信號鏈

理想濾波器和實際濾波器

理想低通濾波器應當具有很陡的過渡帶，其通帶應具有出色的增益平坦度，如圖2 中的磚墻虛線所示。此外，阻帶衰減應將任何殘余帶外信號降低至0。某些常用實際濾波器的響應如圖2 中的彩色線條所示。如果通帶增益不平坦或有紋波，這種響應可能會影響基頻信號。阻帶衰減不是無限的，會限制對帶外噪聲的篩選。過渡帶也可能沒有陡峭的滾降，導致對截止頻率周圍的噪聲衰減不佳。另外，所有非理想濾波器都會引入相位延遲或群延遲。

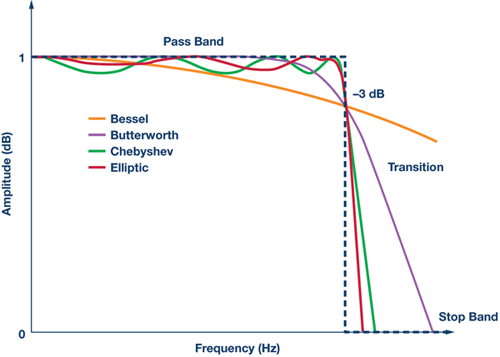
圖2.理想濾波器與實際濾波器的幅度響應對比

模擬濾波器與數字濾波器

模擬低通濾波器可以在ADC 轉換之前消除信號路徑中的高頻噪聲和干擾，幫助避免混疊噪聲污染信號。它還能消除濾波器帶寬之外的過驅信號的影響，避免調制器飽和。發生輸入過壓時，模擬濾波器還能限制輸入電流，衰減輸入電壓。因此，它能保護ADC 輸入電路。疊加于接近滿量程信號上的噪聲尖峰可能會讓ADC 的模擬調制器飽和，必須利用模擬濾波器將其衰減。

由于數字濾波發生在轉換之后，因而可以移除轉換過程中注入的噪聲。在實際應用中，采樣速率遠高于奈奎斯特理論指出的兩倍基頻信號頻率。因此，后置數字濾波器可以利用針對更高信噪比和更高分辨率的濾波技術來降低轉換過程中注入的噪聲，例如：信號帶寬之外的輸入噪聲、電源噪聲、基準源噪聲、數字接口饋通噪聲、ADC 芯片熱噪聲或量化噪聲。

表1簡要列出了模擬濾波器與數字濾波器的優點和缺點。

	模擬濾波器	數字濾波器
設計復雜度	高（對于高性能濾波器）	低
成本	高（取決于所選模擬元件）	低（可用CPU時間）
延遲	低	高
加性噪聲	增加帶內元件熱噪聲	量化可能會引入數字噪聲
ADC輸入保護	是	否
可編程	否	是
漂移誤差	是	否
陳化	是	否
多通道匹配誤差	是	否

表1.模擬濾波器與數字濾波器

模擬濾波器考慮

抗混疊濾波器放在ADC 之前，因此這些濾波器必須為模擬濾波器。理想抗混疊濾波器具有如下特性：通帶內具有單位增益，無增益變化，混疊衰減水平與所用數據轉換系統的理論動態范圍一致。

根據架構不同，ADC 會有不同的輸入電阻，這會影響輸入濾波器設計。以下考慮關系到ADC 模擬輸入濾波器的設計。

與ADC 前端接口的RC 抗混疊濾波器的限制

在Alan Walsh 為Analog Dialogue 雜志撰寫的文章"精密SAR 型模數轉換器的前端和放大器和RC 濾波器設計" 中，有一個針對AD7980ADC 的RC 濾波器應用示例，如圖3 所示。

算出的RC 濾波器是一個低通濾波器，截止帶寬為3.11 MHz。但是，某些設計人員可能會意識到，3.11 MHz 遠大于100 kHz 的輸入信號頻率，因此，該濾波器無法有效降低帶外噪聲。為實現更高動態范圍，可以換用590 Ω 電阻，以獲得100 kHz 的 –3 dB 帶寬。這種方法主要有兩個問題。由于通帶中會有更多衰減，對于AD7980 ADC 示例，100 kHz 附近的幅度衰減最高可達30%，因此，信號鏈精度會大大降低。帶寬越小，則建立時間越長，這使得AD7980 的內部采樣保持電容無法在指定的采集時間內完成充電，因而無法執行下一次有效轉換。這導致ADC 轉換精度降低。

設計人員應當確保ADC 之前的RC 濾波器能在目標采集時間內完全建立。這對需要較大輸入電流或具有等效的較小輸入阻抗的精密ADC 來說異常重要。某些Σ-Δ 型ADC 在無緩沖輸入模式下對輸入RC 值的要求最高。可以將具有較大電阻或電容的超窄低通濾波器放在一般具有較大輸入阻抗的輸入放大器之前。或者可以選擇具有極高輸入阻抗的ADC，例如ADAS3022其輸入阻抗為500 MΩ。

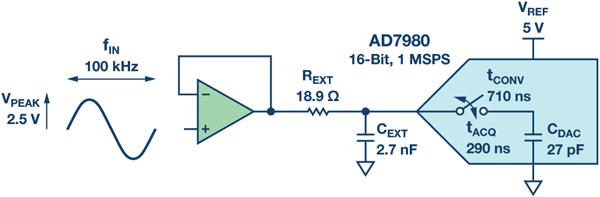
圖3.采用16 位1 MSPS ADC AD7980 的RC 濾波器

1. 多路復用采樣信號鏈的濾波器建立時間

在通道間切換時，多路復用輸入信號通常含有較大的階躍。最差情況下，一個通道處于負滿量程，而下一個通道則處于正滿量程（見圖4）。這種情況下，當多路復用器切換通道時，輸入階躍大小將是ADC 的滿量程。

對于這些通道，可以在多路復用器之后使用一個單通道濾波器，使得設計更簡單，成本更低。如上所述，模擬濾波器必定會引入建立時間。每次多路復用器在通道間切換時，該單通道濾波器都必須充電到所選通道的值，因而會限制吞吐速率。為提高吞吐速率，可以在多路復用器之前為每個通道添加一個濾波器，但這樣做會提高成本。

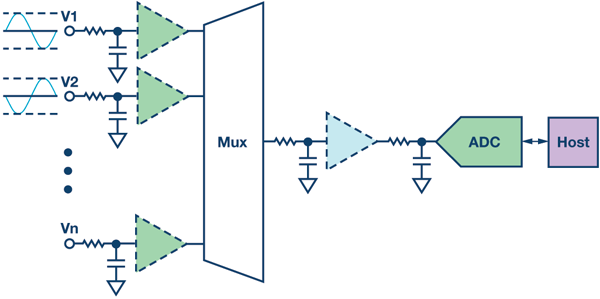
圖4.多路復用輸入信號鏈

2. 通帶平坦度和過渡帶限制與噪聲的關系

遭遇高噪聲的應用，尤其是在接近第一奈奎斯特區邊緣處發生很高干擾的應用，需要滾降厲害的濾波器。然而，人們已從實際模擬低通濾波器得知：從低頻到高頻，幅度會滾下來，并有一個過渡帶。增加濾波器級數或階數可以改善帶內信號的平坦度，并使過渡帶收窄。然而，這些濾波器的設計很復雜，因為它們對增益匹配非常敏感，以至于無法實現數階的衰減幅度。此外，在信號鏈中增加任何元件（如電阻或放大器）都會引入帶內噪聲。

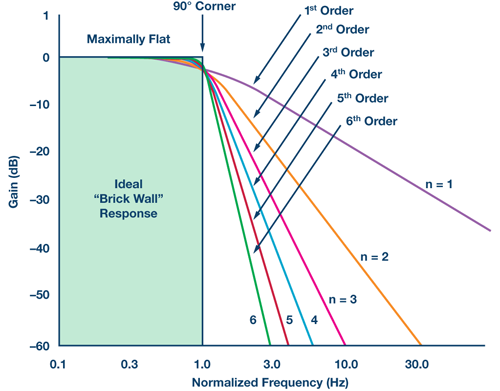
圖5.不同階數的理想巴特沃茲濾波器過渡帶

對于某些具體應用，模擬濾波器設計的復雜度和性能需要進行取舍。例如，在采用AD7606的電力線繼電器保護應用中，對于50 Hz/60 Hz 基頻輸入信號及其相關前五次諧波，保護通道的精度要求低于測量通道。保護通道可以使用一個一階RC 濾波器，而測量通道使用二階RC 濾波器，以便提供更好的帶內平坦度和更急劇的滾落過渡。

3. 同步采樣的相位延遲和匹配誤差

濾波器設計不僅僅關系到頻率設計，用戶可能還需要考慮模擬濾波器的時域特性和相位響應。在某些實時應用中，相位延遲可能非常重要。如果相位隨輸入頻率而變化，那么相位變動將更糟糕。濾波器的相位變化一般用群延遲來衡量。對于非常數群延遲，信號會在時間中擴散，導致脈沖響應變得很差。

對于多通道同步采樣應用，例如電機控制或電力線監控中的相電流測量，還應考慮相位延遲匹配誤差。確保濾波器在多個通道上引起的額外相位延遲匹配誤差可以忽略不計，或者在工作溫度范圍的信號鏈誤差預算范圍內。

4.低失真和低噪聲應用的元件選擇挑戰

對于低諧波失真和低噪聲應用，用戶必須為信號鏈設計選擇合乎要求的元件。模擬電子元件不是完全線性的，會引起諧波失真。Walsh 的文章中討論了如何選擇低失真放大器和如何計算放大器噪聲。放大器等有源元件需要低THD + N，同時也要考慮普通電阻和電容等無源元件的失真和噪聲。

電阻的非線性有兩個來源：電壓系數和功率系數。根據具體應用，高性能信號鏈可能需要使用由特定技術制造的電阻，如薄膜或金屬電阻。如果選擇不當，輸入濾波電容可能會造成顯著失真。如果成本預算允許，聚苯乙烯和NP0/C0G 陶瓷電容是很好的備選元件，可以改善THD。

除放大器噪聲外，電阻和電容也會有電子噪聲，后者是由處于均衡態的電導體內部的電荷載子的熱擾動產生的。RC 電路的熱噪聲有一個簡單的表達式，電阻R 是滿足濾波要求所需要的，同時R 越高，相應的熱噪聲也越大。RC 電路的噪聲帶寬為1/(4RC)。

除放大器噪聲外，電阻和電容也會有電子噪聲，后者是由處于均衡態的電導體內部的電荷載子的熱擾動產生的。RC 電路的熱噪聲有一個簡單的表達式，電阻R 是滿足濾波要求所需要的，同時R 越高，相應的熱噪聲也越大。RC 電路的噪聲帶寬為1/(4RC)。

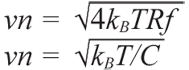
k_B (玻爾茲曼常數) = 1.38065 ×10–23m2kgs–2K–1

T 為溫度(K)

f 為磚墻濾波器近似帶寬

圖6 顯示在EVAL-AD7960FMCZ評估板上，NP0 電容和X7R 電容對THD 性能的影響：(a) 顯示一個10 kHz 正弦波信號音的頻譜，C76 和C77 為1 nF 0603 NP0 電容，而(b) 顯示使用1 nF 0603 X7R 電容時的頻譜。

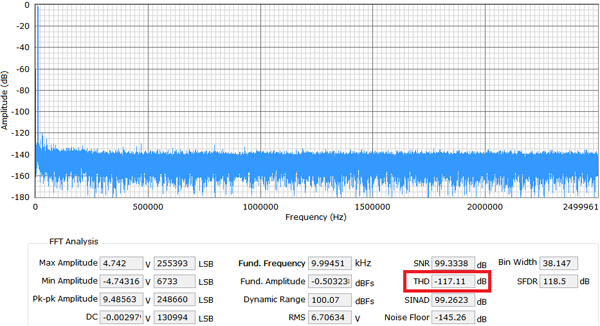
(a) 0603 1n

F NP0 電容

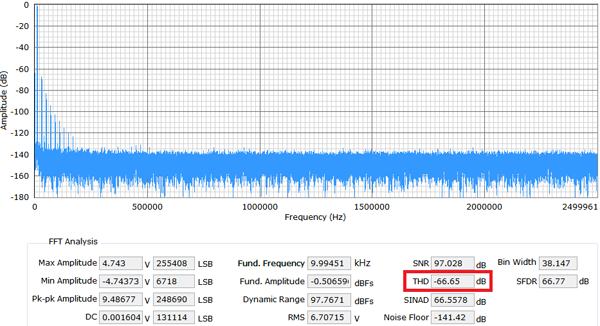
(b) 0603 1nF X7R 電容

圖6.在EVAL-AD7960FMCZ 評估板上NP0 和X7R 電容對THD 的影響

了解前面的設計考慮之后，便可利用ADI 公司的模擬濾波器向導設計有源模擬濾波器。它會根據應用要求計算電容和電阻值，并選擇合適的放大器。

數字濾波器考慮

SAR 型和Σ-Δ 型ADC 正在穩步實現更高的采樣速率和輸入帶寬。以兩倍奈奎斯特速率對一個信號過采樣，會將ADC 量化噪聲能量均勻擴散到兩倍頻段中。這樣便很容易設計數字濾波器來限制數字化信號的頻帶，然后通過抽取來提供所需的最終采樣速率。這種技術可降低帶內量化誤差并提高ADC SNR。它還能放寬濾波器滾降要求，從而減輕抗混疊濾波器的壓力。過采樣降低了對濾波器的要求，但需要更高采樣速率ADC 和更快的數字處理。

1. 對ADC 使用過采樣速率所取得的實際SNR 改善

利用過采樣和抽取濾波器所取得的SNR 改善，可從N 位ADC 的 理論SNR 求得：SNR = 6.02 ×N + 1.76 dB + 10 ×log10[OSR]，OSR = f_s/(2 ×BW)。注意：此公式僅適用于只存在量化噪聲的理想ADC。

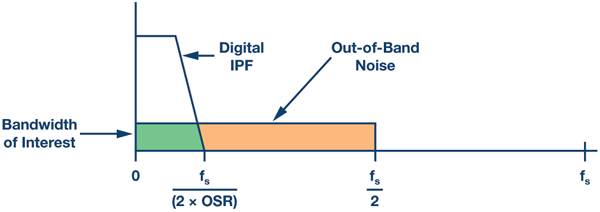
圖7.奈奎斯特轉換器過采樣

還有很多其他因素會將噪聲引入ADC 轉換代碼中。例如：信號源和信號鏈器件的噪聲，芯片熱噪聲，散粒噪聲，電源噪聲，基準電壓噪聲，數字饋通噪聲，以及采樣時鐘抖動引起的相位噪聲。這種噪聲可能會均勻分布在信號頻段中，表現為閃爍噪聲。因此，實際實現的ADC SNR 改善幅度一般低于用公式計算出的值。

2. EVAL-AD7960FMCZ 評估板上利用過采樣實現的動態改善

在應用筆記AN-1279 中，256×過采樣下18 位AD7960 ADC 的實測動態范圍為123 dB。這是用于高性能數據采集信號鏈，如光譜分析、磁共振成像(MRI)、氣相色譜分析、振動、石油/ 天然氣勘探和地震系統等。

如圖8 所示，與理論SNR 改善幅度計算相比，測得的過采樣動態范圍低1 dB 至2 dB。原因是來自信號鏈器件的低頻噪聲限制了總體動態范圍性能。

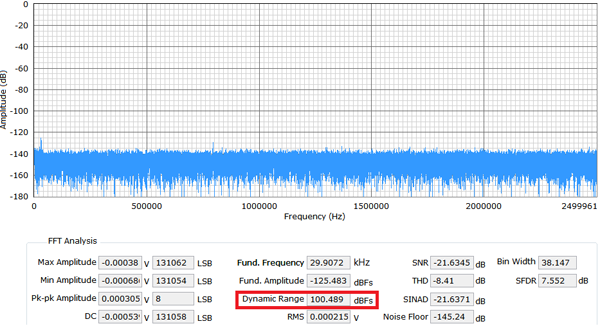
(a) 無OSR 的動態范圍

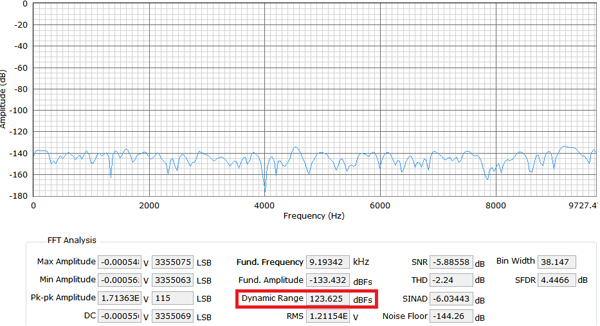
(b) OSR = 256 的動態范圍

圖8.OSR 256 時的動態范圍改善

3. 充分利用SAR 型和Σ-Δ 型ADC 中的集成數字濾波器

數字濾波器通常位于FPGA、DSP 或處理器中。為了減少系統設計工作，ADI 公司提供了一些集成后置數字濾波器的精密ADC。例如，AD7606 集成了一個一階后置數字sinc 濾波器用于過采樣。它很容易配置，只需上拉或下拉OS 引腳。Σ-Δ 型 ADC AD7175-x 不僅有傳統sinc3 濾波器，還有sinc5 + sinc1 和增強型50 Hz/60 Hz 抑制濾波器。AD7124-x 提供快速建立模式（sinc4 + sinc1 或sinc3 + sinc1 濾波器）功能。

4.多路復用采樣ADC 的延遲取舍

延遲是數字濾波器的一個缺點，它取決于數字濾波器階數和主時鐘速率。對于實時應用和環路響應時間，應當限制延遲。數據手冊所列的輸出數據速率是指在單一通道上執行連續轉換時轉換結果有效的速率。當用戶切換到另一通道時，建立Σ-Δ 調制器和數字濾波器還額外需要些時間。與這些轉換器相關的建立時間是指通道變更之后輸出數據反映輸入電壓所需的時間。通道變更之后，為精確反映模擬輸入，必須清除數字濾波器中與前一模擬輸入相關的全部數據。

以前，Σ-Δ 型ADC 的通道切換速度比數據輸出速率要小得多。因此，在多路復用數據采集系統等切換應用中，必須明白：獲得轉換結果的速率要比對單一通道連續采樣時可達到的轉換速率低好幾倍。

ADI 公司的某些新型Σ-ΔADC（如AD7175-x）內置優化的數字濾波器，可減少通道切換時的建立時間。AD7175-x 的sinc5 + sinc1 濾波器主要用于多路復用應用，在10 kSPS 和更低的輸出數據速率時，可實現單周期建立。

5.數字濾波器通過抽取避免混疊

很多文章都討論過，過采樣頻率越高，模擬濾波器設計就越容易。當采樣速率高于滿足奈奎斯特準則所需的速率時，便可使用較簡單的模擬濾波器來避免受到極高頻率所產生的混疊影響。很難設計一個能夠衰減所需頻段而不失真的模擬濾波器，但很容易設計一個利用過采樣抑制較高頻率的模擬濾波器。這樣便很容易設計數字濾波器來限制轉換信號的頻帶，然后通過抽取來提供所需的最終采樣速率，但又不會喪失所需信息。

實施抽取之前，需要確保這種重新采樣不會引入新的混疊問題。抽取之后，確保輸入信號符合奈奎斯特關于采樣速率的理論。

EVAL-AD7606/EVAL-AD7607/EVAL-AD7608EDZ 評估板可以每通道200 kSPS 的速率運行。在下面的測試中，配置其采樣速率為6.25 kSPS，過采樣比為32。然后，將一個3.5 kHz –6 dBFS 正弦波施加于AD7606。圖9 顯示2.75 kHz (6.25 kHz –3.5 kHz) 處有一個–10 dBFS 混疊鏡像。因此，若ADC 之前沒有合格的抗混疊模擬濾波器，當使用過采樣時，數字濾波器就可能會因為抽取而引起混疊鏡像。應使用模擬抗混疊濾波器來消除這種疊加于模擬信號上的噪聲尖峰。

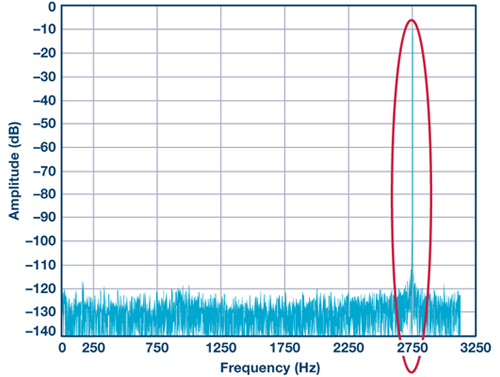
圖9.OSR 抽取采樣率小于奈奎斯特頻率時的混疊

結論

本文討論的挑戰和考慮可幫助設計人員設計出實用的濾波器以實現精密采集系統的目標。模擬濾波器必須在不違反系統誤差預算的條件下與SAR 型或Σ-Δ 型ADC 的非理想輸入結構接口，數字濾波器不應在處理器端引起誤差。這不是簡單的任務，必須在系統規格、響應時間、成本、設計工作量和資源等方面做出權衡。

參考電路

Holdaway, Mark. "ADC 用抗混疊濾波器設計"。EDN，2006 年。
Walsh, Alan。 精密SAR 型模數轉換器的前端放大器和RC 濾波器設計。Analog Dialogue，第46 卷第4 期，2012 年。
Wescott，Tim；Wescott 設計服務。"采樣：奈奎斯特沒說什么 以及怎么辦"。Wescott 研討會，2015 年。
巴特沃茲濾波器設計。
模擬和數字抗混疊濾波。