0 引言
隨著航空電子偵察技術(shù)的發(fā)展,機(jī)載測(cè)向系統(tǒng)以其作用范圍大。偵測(cè)距離遠(yuǎn)。機(jī)動(dòng)性強(qiáng)和可實(shí)現(xiàn)單機(jī)對(duì)地面目標(biāo)定位等優(yōu)點(diǎn),能夠完成地面通信電子戰(zhàn)設(shè)備所不能完成的遠(yuǎn)距離。大區(qū)域作戰(zhàn)任務(wù),正越來越受到國內(nèi)外關(guān)注。但是在實(shí)際工程應(yīng)用中,機(jī)載測(cè)向中面臨著以下幾個(gè)方面的問題。
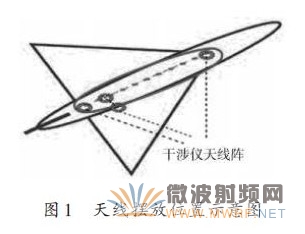
(1)機(jī)載平臺(tái)可供布設(shè)天線陣列的有效空間。允許的天線陣元尺寸和數(shù)量十分有限,不能使用大基礎(chǔ)天線陣;同時(shí)飛機(jī)結(jié)構(gòu)面多為弧面,這也限制了均勻圓形陣向低頻段擴(kuò)展的可能。本文考慮到飛機(jī)本身的結(jié)構(gòu)特點(diǎn)是機(jī)身橫向窄縱向長(zhǎng),為有效利用飛機(jī)機(jī)腹的空間,提出了均勻橢圓布陣的形式,通過仿真分析了橢圓陣列孔徑與波長(zhǎng)之比對(duì)入射角度的估計(jì)性能影響。
(2)現(xiàn)代雷達(dá)系統(tǒng),通常采用在目標(biāo)雷達(dá)周圍配備有源誘餌進(jìn)行保護(hù),這就要機(jī)載測(cè)向系統(tǒng)有高的分辨力,但是基于相位干涉儀的測(cè)向方法只能實(shí)現(xiàn)對(duì)單個(gè)信號(hào)的測(cè)向,而空間譜估計(jì)測(cè)向法可以實(shí)現(xiàn)對(duì)一個(gè)波束寬度內(nèi)多個(gè)入射信號(hào)的來波方向估計(jì),所以有效地提高空間譜估計(jì)方法在實(shí)際測(cè)向系統(tǒng)中的分辨力至關(guān)重要。
(3)在實(shí)際測(cè)向中天線陣列通道幅相失衡。天線陣元的互耦等會(huì)導(dǎo)致測(cè)向性能的下降,所以亟需采用有效的校正方法來改善測(cè)向性能。
本文重點(diǎn)研究前兩個(gè)方面的問題。
1 機(jī)載平臺(tái)測(cè)向天線陣設(shè)計(jì)
1.1 相關(guān)干涉儀測(cè)向技術(shù)
測(cè)向原理如下:在測(cè)向天線陣工作頻率范圍內(nèi)和0~360°方向上,各按一定規(guī)律設(shè)點(diǎn),同時(shí)在頻率間隔和方位間隔上建立樣本群,在測(cè)向時(shí),將所得的數(shù)據(jù)和樣本群進(jìn)行相關(guān)運(yùn)算和差值處理,以獲得來波信號(hào)方向,可以實(shí)現(xiàn)寬頻帶范圍內(nèi)無模糊測(cè)向,對(duì)陣列的擺放形式?jīng)]有特殊要求。
基于相位差擬合的相關(guān)干涉儀代價(jià)函數(shù)為:

式中:θ為觀測(cè)相位差向量;θj為對(duì)應(yīng)于(θ,φ)方向的相位差向量,使得ρj最大值所對(duì)應(yīng)的原始相位樣本值就是實(shí)際入射信號(hào)的方位。
1.2 測(cè)向天線陣設(shè)計(jì)及仿真
針對(duì)機(jī)載平臺(tái)的特點(diǎn),給出了橢圓天線陣列擺放示意,如圖1所示。
設(shè)M個(gè)天線陣元均勻分布在一個(gè)橢圓圓周上,以幾何中心為參考點(diǎn),則陣列的方向向量a(θ)可表示為:
設(shè)a(θA),a(θB )是均勻橢圓陣列上的2個(gè)方向向量,則相關(guān)系數(shù)為:
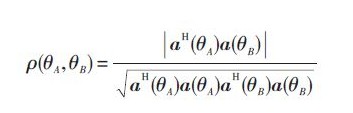
仿真分析1:
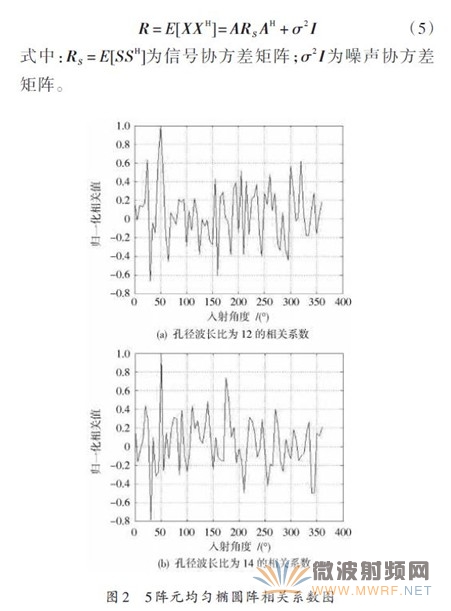
設(shè)橢圓陣孔徑與波長(zhǎng)之比(d λ)分別為12和14,信號(hào)入射方向?yàn)?0°,5元均勻橢圓陣的相關(guān)系數(shù)圖如圖2所示。
可見,相關(guān)系數(shù)的最大值在方位角50°處。從仿真圖2可得如下結(jié)論:d λ越大,主瓣越窄,方位測(cè)量精度越高;去除測(cè)向模糊就是要求相關(guān)系數(shù)圖的主瓣與副瓣的高度易于分辨。MUSIC算法其分辨力與陣列孔徑成正比。也就是說當(dāng)可利用的陣列孔徑受限時(shí),會(huì)影響到分辨力,但為了提高系統(tǒng)的分辨力而增大天線盤的孔徑代價(jià)太大。所以要在不需要通過增大陣列的物理孔徑來實(shí)現(xiàn)MUSIC算法的分辨力上下功夫。
2 MUSIC算法分辨能力2.1 MUSIC算法原理及分辨性能設(shè)有P個(gè)不相關(guān)窄帶入射到M元遠(yuǎn)場(chǎng)線陣上,則陣列輸出向量為:
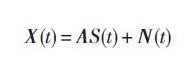
式中:X(t)為M × 1維的陣列輸出向量;A為M × P維的陣列流型,它是輻射信號(hào)入射角α和β的函數(shù);S(t)為P × 1維的入射信號(hào)向量;N(t)為M × 1維的噪聲向量。由于信號(hào)與噪聲相互獨(dú)立,接收數(shù)據(jù)的協(xié)方差矩陣為:
對(duì)R進(jìn)行特征分解,P個(gè)大特征值對(duì)應(yīng)的特征向量Us = [e1,e2 ,…,ep]張成信號(hào)子空間;M – P個(gè)小特征值對(duì)應(yīng)的特征向量UN = [ep + 1,ep + 2 ,…,eM ]張成噪聲子空間,兩個(gè)子空間正交。在噪聲子空間上投影為0的陣列流形所對(duì)應(yīng)的方向就是信號(hào)的DOA,MUSIC算法通過搜索式(6)的極大值點(diǎn)來獲得輻射信號(hào)的DOA:

仿真分析2:
天線陣列采用均勻的5元橢圓陣,信噪比為20 dB,快拍數(shù)為1 000,取三個(gè)輻射信號(hào)(45°,75°),(45°,78°),(38°,30°),仿真結(jié)果如圖3所示。

仿真分析2:
天線陣列采用均勻的5元橢圓陣,信噪比為20 dB,快拍數(shù)為1 000,取三個(gè)輻射信號(hào)(45°,75°),(45°,78°),(38°,30°),仿真結(jié)果如圖3所示。

仿真分析3:
天線盤孔徑對(duì)MUSIC算法分辨力的影響。天線陣列形式采用均勻的5 元橢圓陣,取兩個(gè)輻射信號(hào)分別為(45°,75°),(45°,78°),即兩個(gè)入射角間距為3°,依據(jù)式(7)對(duì)不同孔徑與波長(zhǎng)比(d λ)條件下的分辨能力進(jìn)行仿真,如圖4所示。

從圖4可以看出,MUSIC算法分辨能力隨天線盤孔徑的增大而提高。故可以考慮通過增大天線盤孔徑來提高M(jìn)USIC算法的分辨力,但天線盤的尺寸受限,不可以無限增大。鑒于四階累積量的陣列具有擴(kuò)展特性,利用它來增加天線盤的孔徑,以提高陣列的分辨力。
2.2 四階累積量2D-MUSIC
2.2.1 四階累積量2D-MUSIC的陣列擴(kuò)展特性及原理
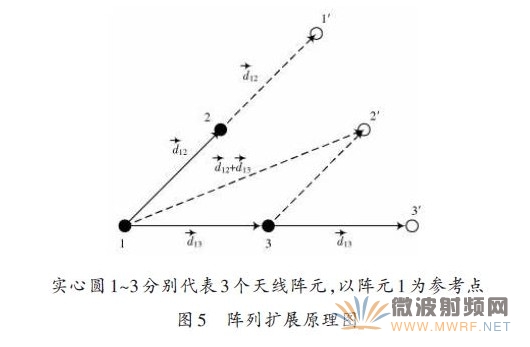
王永良等人給出了四階累積量特性的詳細(xì)理論推導(dǎo),這里不再重復(fù)闡述。如圖5所示,以空間中3個(gè)天線陣元為例,對(duì)四階累積量的陣列擴(kuò)展特性進(jìn)行說明。
其陣列導(dǎo)向矢量可以表示為:
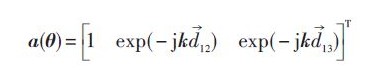
式中:k 表示輻射信號(hào)入射角度矢量;d12和d13分別代表陣元2.3相對(duì)參考陣元1的位置矢量。
利用四階累積量的擴(kuò)展特性對(duì)圖5 的陣列擴(kuò)展后的導(dǎo)向矢量為:
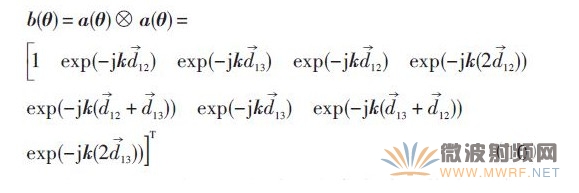
由圖5可以看出,空間中3個(gè)真實(shí)陣元構(gòu)成的陣列經(jīng)四階累積量陣列擴(kuò)展后構(gòu)成了6個(gè)陣元的虛擬陣列,陣列孔徑擴(kuò)大1倍,然后利用擴(kuò)展后的陣列對(duì)輻射信號(hào)的入射角度進(jìn)行估計(jì),以達(dá)到提高分辨力的效果。
基于四階累積量的MUSIC算法也是利用信號(hào)子空間與噪聲子空間的正交性,其空間譜函數(shù)表達(dá)式為:
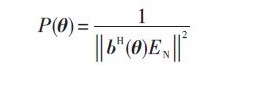
通過譜峰搜索,找到P個(gè)極大值對(duì)應(yīng)的角度,實(shí)現(xiàn)對(duì)輻射信號(hào)的二維DOA估計(jì)。
仿真分析4:
以均勻5元橢圓陣為例驗(yàn)證四階累積量的MUSIC算法和MUSIC算法分辨性能,同樣采用的信噪比為20 dB,快拍數(shù)為1 000,取三個(gè)輻射信號(hào)(45°,75°),(45°,80°),(38°,30°),仿真結(jié)果如圖6所示。
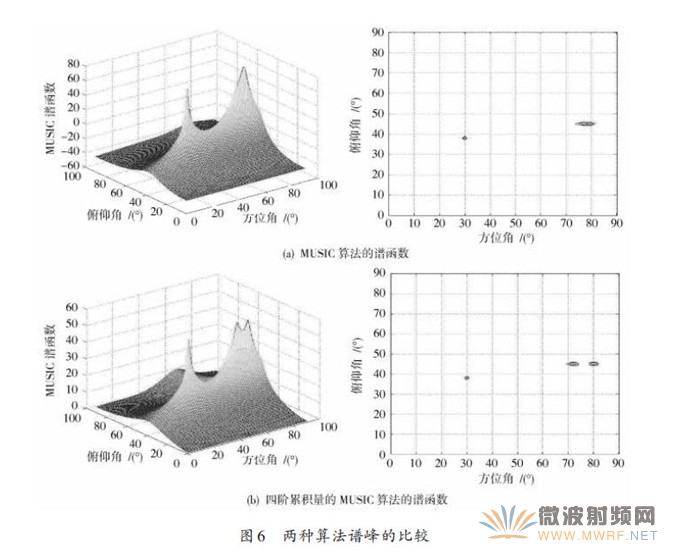
由圖6(a)可以看出,采用MUSIC 算法對(duì)入射角度于(45°,75°),(45°,80°)進(jìn)行估計(jì)失敗,而采用四階累積量MUSIC算法進(jìn)行估計(jì)時(shí)得到了兩個(gè)尖銳的譜峰,通過四階累積量MUSIC 算法的譜函數(shù)搜索得到入射角度為(45°,75.5°),(45°,80°)。由此可見,采用四階累積量MUSIC算法使得陣列孔徑得到了有效的擴(kuò)展,其分辨力高于MUSIC算法。
2.2.2 四階累積量2D-MUSIC算法與MUSIC算法計(jì)算量分析
MUSIC算法通過對(duì)接收數(shù)據(jù)的協(xié)方差矩陣和進(jìn)行特征分解,運(yùn)算量為ο(M2 K) + ο(M3)。計(jì)算一個(gè)四階累積量需要9L次復(fù)乘運(yùn)算,其中L表示快拍數(shù),奇異值分解的計(jì)算量約為ο(M6),其中M表示所構(gòu)造的累積量數(shù)據(jù)矩陣的維數(shù)。其實(shí)從四階累積量MUSIC 算法陣列擴(kuò)展原理圖可知,采用該算法進(jìn)行譜峰搜索所用的陣元個(gè)數(shù)遠(yuǎn)遠(yuǎn)的多于原陣列的陣元個(gè)數(shù)。譬如在圖6(b)的仿真實(shí)驗(yàn)中,需要對(duì)方位角0~360°,仰角0~90°范圍內(nèi)進(jìn)行譜峰搜索,那么將方位角和仰角的搜索步長(zhǎng)分別設(shè)置為1°,0.5°,則需要361 × 181次譜函數(shù)計(jì)算,而譜函數(shù)計(jì)算量與陣列導(dǎo)向矢量有關(guān),即與陣元數(shù)量有關(guān)。也就是說雖然四階累積量MUSIC算法引入虛擬陣元擴(kuò)大孔徑使得分辨力提高,但也導(dǎo)致譜峰搜索的計(jì)算量大增。
仿真分析5:
計(jì)算量仿真統(tǒng)計(jì)分析。對(duì)不同快拍數(shù)下這兩個(gè)算法所占用的計(jì)算時(shí)間進(jìn)行統(tǒng)計(jì),各算法計(jì)算時(shí)間均由100次Monte-Carlo實(shí)驗(yàn)進(jìn)行平均得到,見表1.
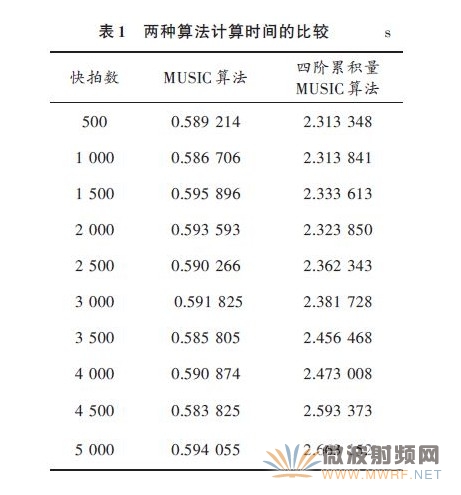
由表1可以看出,四階累積量MUSIC算法的計(jì)算時(shí)間大約是MUSIC 算法的4 倍。但文獻(xiàn)[5]中從算法的角度給出了一種快速去冗余的方法,將M2 × M2 的四階累積量矩陣轉(zhuǎn)化為(2M – 1) × (2M – 1)的四階累積量矩陣,從而大大降低了計(jì)算量。同時(shí)相信隨著DSP 和FPGA 等數(shù)據(jù)處理飛速發(fā)展,四階累積量MUSIC算法的運(yùn)算時(shí)間會(huì)減小,從而更好的將四階累積量MUSIC算法應(yīng)用于陣列信號(hào)處理中。
3 結(jié)語
根據(jù)機(jī)載干涉儀測(cè)向系統(tǒng)面臨著可供布陣的空間有限,不能像陸基一樣布陣成理想陣列,考慮到飛機(jī)機(jī)身橫向較窄而縱向很長(zhǎng)給出了橢圓陣列模型,通過仿真分析了橢圓孔徑與波長(zhǎng)之比對(duì)入射角度的估計(jì)性能,發(fā)現(xiàn)了測(cè)向精度受陣列有效孔徑的限制。然而在實(shí)際機(jī)載測(cè)向系統(tǒng)中通過增大陣列孔徑來提高分辨力估計(jì)性能是不現(xiàn)實(shí)。考慮通過四階累積量陣列擴(kuò)展特性來引入虛擬陣元,這樣就可以在受限平臺(tái)上實(shí)現(xiàn)天線盤孔徑大增,完成一。二維DOA高精度估計(jì)。惟一的缺點(diǎn)就是計(jì)算量大,所以今后的努力方向是不僅要從改進(jìn)算法的角度來減少四階累積量的運(yùn)算量,也從用DSP來實(shí)現(xiàn)的角度縮短執(zhí)行時(shí)間。

 粵公網(wǎng)安備 44030902003195號(hào)
粵公網(wǎng)安備 44030902003195號(hào)