一、引言

通常我們在分析有反饋行波管振蕩系統(tǒng)的振蕩建立過程時(shí)，可以利用行波管的輸入-輸出特性以及反饋系數(shù)計(jì)算出每次循環(huán)后行波管的輸出功率。這樣的過程可以用下面的離散化的演化方程來描述。

P_out,n=f(P_in,n)，

P_in,n=P_out,n+Fd，

其中，P_out、P_in、Fd以dB計(jì)。

顯然這是一個(gè)非線性系統(tǒng)，這類似于一維拋物線映射。只要關(guān)系式f(P_in)滿足一定的條件及Fd為合適的值時(shí)，這樣的反饋系統(tǒng)就可以出現(xiàn)混沌現(xiàn)象。基于上述考慮我們用實(shí)驗(yàn)的方法對此反饋系統(tǒng)進(jìn)行了實(shí)驗(yàn)研究。觀察到行波管可以工作在三種狀態(tài)下：單頻振蕩、分岔及混沌。

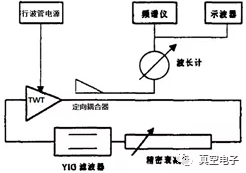
圖1、實(shí)臉裝置簡圖

二、實(shí)驗(yàn)及數(shù)據(jù)

為了觀察行波管中的混沌現(xiàn)象，我們采用了圖1所示的實(shí)驗(yàn)裝置。圖1中的行波管為某一儲(chǔ)頻行波管,此行波管在Uh=2047V,  Ic=4.0mA 下的輸入-輸出特性曲線如圖2所示。由圖2可知此管的輸入-輸出曲線 的后半段隨輸入功率的增加，輸出功率下降較快，符合產(chǎn)生混沌的要求。

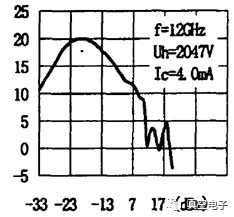
圖2、某行波管的輸入-輸出特性曲線

實(shí)驗(yàn)觀察時(shí)，首先使反饋量為最小，然后逐漸增加反饋量,同時(shí)在頻譜儀上觀察行波管的輸出結(jié)果。在增大反饋量的過程中可以看到：首先為單根譜線，其次是等間隔的多根譜線（兩分岔），且譜線的高度由中間向兩邊逐漸降低，再次在原多根譜線中央出現(xiàn)新的譜線（第1次倍周期分岔），而后幾次在原譜線中央出現(xiàn)新的譜線（多次倍周期分岔），最后出現(xiàn)中央高兩邊低的雜亂譜線（混沌），如圖4所示。

實(shí)驗(yàn)時(shí)我們在7.9-13.0GHz范圍內(nèi)觀察了改變反饋量時(shí)，行波管從單頻振蕩到分岔再到混沌的發(fā)展過程。發(fā)現(xiàn)只有在9-12.6GHz范圍內(nèi)才能出現(xiàn)混沌。我們在此范圍內(nèi)每隔500MHz進(jìn)行一次觀察。觀察結(jié)果如表1所示。

表1

在有反饋的情況下,行波管的輸出可以計(jì)為A(t)cos(ωt)。在N周期分岔時(shí)，設(shè)幅度分別為A1，A2，…，As，…，AN，作幅度的傅里葉分析結(jié)果為:

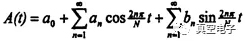
其中

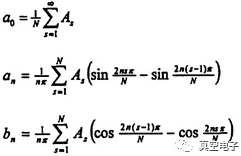
由以上的分析，譜線的間隔與反饋系統(tǒng)的延時(shí)有關(guān)。實(shí)驗(yàn)中改換不同長度的電纜作試驗(yàn)，證實(shí)了這一點(diǎn)。實(shí)驗(yàn)采用的反饋系統(tǒng)延時(shí)為39.0-40.0ns，測得兩分岔時(shí)，譜線的間隔寬度為12.0-13.0MHz。

以上作傅里葉分析時(shí)，未考慮噪聲的影響，可得出在兩分岔時(shí)主譜線與相鄰的副譜線間隔應(yīng)是兩相鄰的副譜線之間距的一半。而在兩分岔時(shí)實(shí)驗(yàn)中觀察到的是，所有的譜線間距是相等的。這是因?yàn)閷?shí)際系統(tǒng)是有噪聲的，造成在一個(gè)循環(huán)周期內(nèi)行波管的輸出不恒定所引起的。

實(shí)際系統(tǒng)中用了YIG磁調(diào)濾波器，不用此濾波器能不能觀察到從分岔到混沌的發(fā)展過程呢？回答是能。只是不用濾波器時(shí)，能量分布在較寬的頻帶中，譜線的高度要大幅度的降低，如圖3所示。而用此濾波器能起到集中能量的目的，同時(shí)控制混沌的中心頻率，如圖4所示。

實(shí)驗(yàn)觀察表明，螺旋線電壓的微小變化，就可明顯影響行波管中的混沌產(chǎn)生。利用此性能，可以在螺旋線上加10伏左右的調(diào)制電壓對行波管產(chǎn)生的混沌進(jìn)行調(diào)制，從而產(chǎn)生強(qiáng)烈的閃爍效應(yīng)，這對電子對抗是很有用的。

圖3、無濾波器時(shí)的混沌頻譜

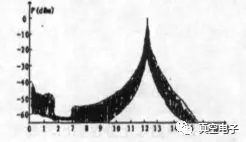
圖4、有濾波器時(shí)的混沌頻譜

三、結(jié)束語

行波管中的混沌現(xiàn)象研究開始的較晚，但在海灣戰(zhàn)爭之后美國及西方各國一直在強(qiáng)化這方面的研究工作。

本文介紹了用實(shí)驗(yàn)方法對行波管中的混沌現(xiàn)象進(jìn)行研究得出的一些結(jié)果。這對進(jìn)一步探索研究行波管中的混沌現(xiàn)象有很大的作用。利用行波管中混沌現(xiàn)象產(chǎn)生的微波噪聲，可以制成噪聲雷達(dá)，提高雷達(dá)的抗干擾性，也可以作為電子對抗中干擾機(jī)的噪聲源，因此對行波管中的混沌現(xiàn)象的進(jìn)一步研究是有現(xiàn)實(shí)意義及應(yīng)用前景的。