由于微波頻段存在趨膚效應，導致微波器件導體內的電流通常集中在表面微米級的厚度內，這是大家所熟知的概念。依據這一原理，業界通常采用下述方法來改善微波器件的損耗，同時降低器件成本：在導體表面（比如鋁合金）沉積厚度約為數個趨膚深度的良導體層（比如鍍金、鍍銀）。這一原理也同樣應用在改善微波無源器件的無源互調性能方面：低互調器件通常采用鍍銀表面。

為了衡量導體材料的損耗性能，人們定義了表面電阻R的概念：

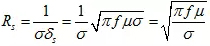
換句話說，表面電阻反比于電導率與趨膚深度之乘積。依據這一概念，可以方便地對器件損耗進行評估。以矩形波導為例，如果只考慮矩形波導寬邊的損耗，則在工作于基模TE10的條件下，波導傳輸線的損耗可以按下式計算：

相位常數的計算方法：

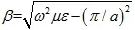
對于趨膚深度的形象理解是：由于電磁波在良導體內部呈現指數衰減，當電磁波滲入導體內部一個趨膚深度的厚度時，電磁波幅度將衰減1/e，也就是36.8%。如果導體厚度達到三個趨膚深度及以上，通常就認為電磁波幅度衰減為零。

以上是我們對于導體損耗與趨膚深度關系的通常認識，下面本文要討論的問題是：如果良導體的厚度等于趨膚深度甚至小于趨膚深度，電磁波會穿透良導體嗎？上面提到的“表面電阻等于電導率與趨膚深度乘積之倒數”該如何應用于導體厚度小于趨膚深度的情形？

實際上，教科書中有關趨膚深度的討論是針對導體厚度無限大的理想模型來進行的。當導體厚度等于趨膚深度甚至遠小于趨膚深度而演變為導電薄膜時，電磁波滲入導體內部以后，將在出射導體薄膜時由于導體薄膜阻抗與空氣阻抗的失配而發生發射（假設導電薄膜背面為空氣介質）。因此，即便導電薄膜的厚度只有一個趨膚深度，此時電磁波的衰減量也不再是上文中所說的36.8%。

依據A E Kaplan的論文《on the reflectivity of metallic films at microwave and radio frequencies》，在自由空間中，電磁波垂直入射導電薄膜時，其功率透射系數可按下式計算：

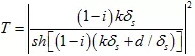
下圖給出了依據該理論得到的金屬鋁厚度對電磁波衰減量的影響規律（電導率為38.6 MS/m，頻率為10 GHz）。

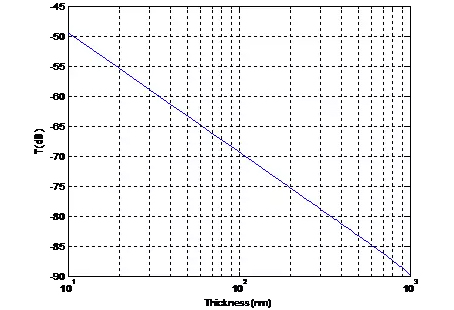
圖1、導電薄膜對電磁波的衰減

由上圖可見，即便鋁膜厚度只有10 nm，其對10 GHz電磁波的衰減也可以達到50 dB，遠大于我們通常從趨膚深度角度所理解的衰減量。

實際上，對于導電薄膜的情形，表面電阻可表示為：

亦即，假設矩形波導的壁厚小于趨膚深度，則計算其導體損耗時，需要將教科書中表面電阻公式中的趨膚深度替換為薄膜厚度。下面，我們給出HFSS的仿真結果，并與理論計算結果對比。電磁波形如圖2所示，類似地，這里僅考慮波導寬邊的損耗。仿真結果如圖3所示（圖中loss項表示輻射損耗；黑色線對應左側縱坐標，紅色線對應右側縱坐標）：當電導率為0.5 MS/m時，輻射損耗顯著，且隨膜厚增加而減??；而當電導率為30 MS/m時，輻射損耗明顯降低。

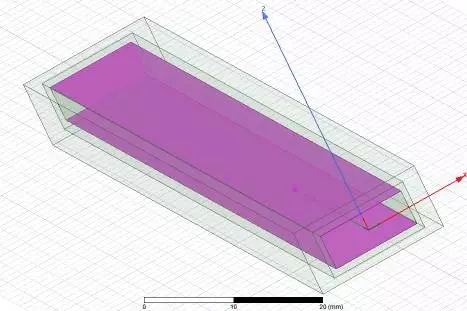
圖2、寬邊為導電薄膜的矩形波導模型

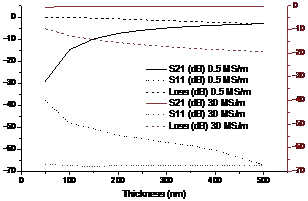
圖3、電導率及膜厚對矩形波導S參數及輻射損耗的影響仿真結果

圖4給出了HFSS仿真與理論計算結果的對比：采用電導率與膜厚定義的表面電阻得到的理論計算結果與HFSS仿真結果吻合良好，表明針對導電薄膜的情形，其表面電阻應為電導率與膜厚乘積的倒數。

圖4、HFSS仿真與理論計算的對比

主要結論：如果良導體的厚度等于趨膚深度甚至小于趨膚深度，電磁波仍然會穿透良導體，但是遠小于我們通常從趨膚深度角度所理解的衰減量；“表面電阻等于電導率與趨膚深度乘積之倒數”對于導電薄膜的情形，應當替換為“表面電阻等于電導率與膜厚乘積之倒數”。