做OFDM通信少不了頻譜分析，基帶信號DA后的頻譜，以及基帶數字上變頻后的DA信號都要頻譜分析。我覺得其實做任何工程都是這樣，先規定實施方案，然后仿真成功，再實際開發，不過也可以一邊開發，一邊仿真，開發結果要與仿真預期結果一致。

所以分析與仿真工具MATLAB就很重要了，既可以仿真，又可以通過示波器或其他方法把實際信號采下來分析。

matlab使用FFT函數分析信號頻譜

一般我使用的FFT分析頻譜流程如下：

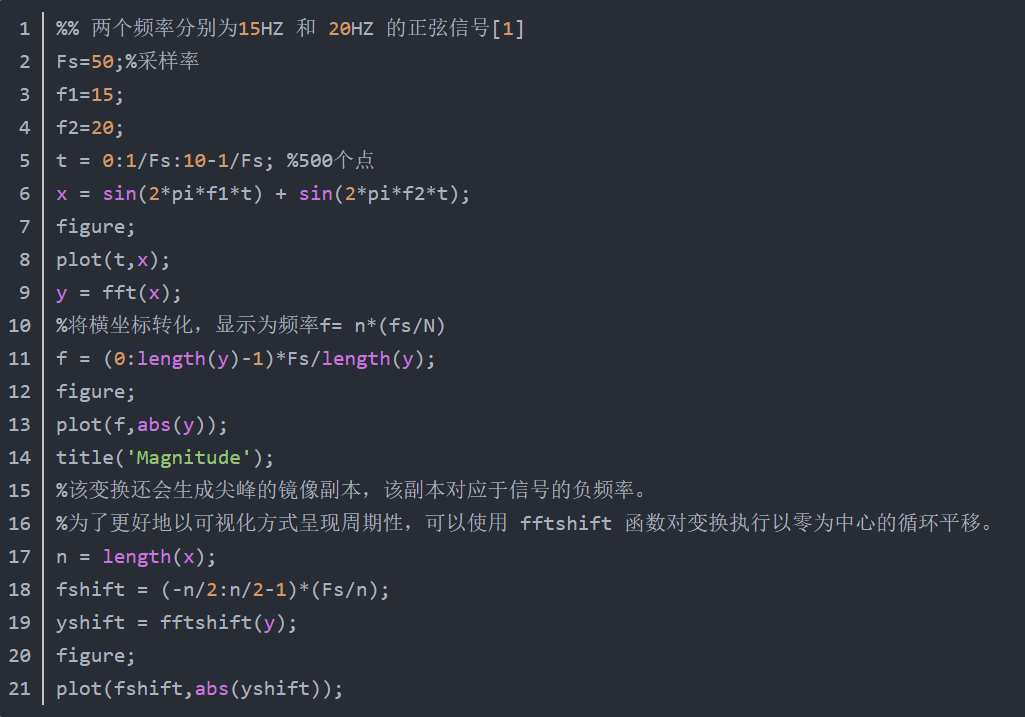
其中有3個注意的點：

1.FFT的結果看的是頻譜，所以怎么把橫坐標的值從原來的FFT點數0:N-1轉換為頻率值呢？

首先要引出頻譜分辨率的概念，即分辨兩個不同頻率信號的最小間隔，FFT結果相鄰點間的間隔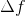。因為N點FFT對應采樣率為fs的序列，其頻率分辨率為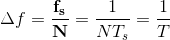,其中Ts為采樣周期，T為整個序列的時間長度。有關頻率分辨率的就不多說了。所以我們橫坐標轉換為：f = (0:length(y)-1)*Fs/length(y);

2.直接FFT的結果里怎么又多余的信號頻率（鏡像頻率）圖2？

DFT具有對稱性，因為其是周期序列DFS在一個周期內的點，時域序列是有限長實序列，DFT的結果的實部周期偶對稱，虛部周期奇對稱，也就是模值周期偶對稱，相位周期奇對稱。其實從奈奎斯特定律也可以看出，fs>=2f，fs的采樣率最多也就顯示fs/2的真實頻率（感性理解哈哈）。
所以程序處理方式就是周期延拓后取-N/2:N/2-1.用到函數fftshift()，結果如圖3.如注釋所述：
%該變換還會生成尖峰的鏡像副本，該副本對應于信號的負頻率。
%為了更好地以可視化方式呈現周期性，可以使用 fftshift 函數對變換執行以零為中心的循環平移。

其實這和設計數字濾波器IIR與FIR也一樣，采樣率為fs的信號，設計的濾波器的通帶阻代也限制在0-fs/2內。

3.程序中的信號幅度值都是1，500點的FFT畫出來的幅度值怎么變成了250，應該是1吧？

是的，應該是1。所以怎么變換為1呢，注意到FFT的結果是偶對稱的，且其反應的真實頻譜是0-fs/2。所以需要的操作是直接取0-N/2的FFT結果，乘以2，然后除以N。即2*abs(y(1:N/2+1))/N，在上面的程序下接著寫：

注意到要除以N，也就是FFT的長度，為什么除以N，這個有很多說法，我自己理性理解的也不透徹，所以這里就不解釋了自行百度（我只能結合本例子感性理解哈哈）。

結果如圖4，可見橫坐標頻率是0-25，縱坐標信號的幅度為1.

然而，有不少人（包括我）平時分析信號都是直接FFT畫頻譜：圖2，且看幅值都是看相對的大小，或者有沒有頻率分量，就很少做圖3與圖4的變換。但是我不知道其中的緣由，今天終于明白了。

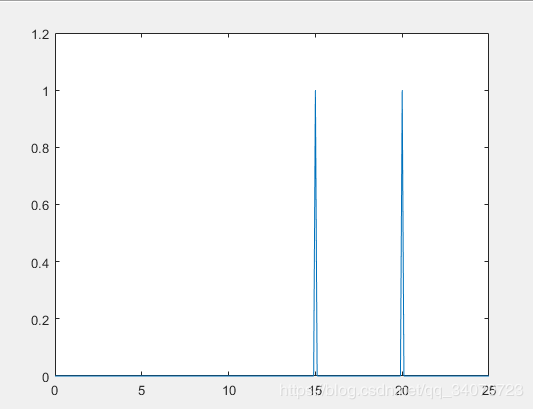
圖4 FFT所反映的真正的頻譜幅值

參考資料

[1]傅里葉變換 - MATLAB & Simulink - MathWorks 中國
[2]快速傅里葉變換- MATLAB fft - MathWorks 中國