Matlab可以說是一個非常有用且功能齊全的工具,在通信、自控、金融等方面有廣泛的應(yīng)用。
本文討論使用Matlab對信號進行頻域分析的方法。
說到頻域,不可避免的會提到傅里葉變換,傅里葉變換提供了一個將信號從時域轉(zhuǎn)變到頻域的方法。之所以要有信號的頻域分析,是因為很多信號在時域不明顯的特征可以在頻域下得到很好的展現(xiàn),可以更加容易的進行分析和處理。
FFT
Matlab提供的傅里葉變換的函數(shù)是FFT,中文名叫做快速傅里葉變換。快速傅里葉變換的提出是偉大的,使得處理器處理數(shù)字信號的能力大大提升,也使我們生活向數(shù)字化邁了一大步。
接下來就談?wù)勅绾问褂眠@個函數(shù)。
fft使用很簡單,但是一般信號都有x和y兩個向量,而fft只會處理y向量,所以想讓頻域分析變得有意義,那么就需要用戶自己處理x向量
一個簡單的例子
從一個簡單正弦信號開始吧,正弦信號定義為:
y(t)=2sin?(2πf0t)
我們現(xiàn)在通過以下代碼在Matlab中畫出這個正弦曲線
1 fo = 4; %frequency of the sine wave2 Fs = 100; %sampling rate
3 Ts = 1/Fs; %sampling time interval
4 t = 0:Ts:1-Ts; %sampling period
5 n = length(t); %number of samples
6 y = 2*sin(2*pi*fo*t); %the sine curve
7
8 %plot the cosine curve in the time domain
9 sinePlot = figure;
10 plot(t,y)
11 xlabel('time (seconds)')
12 ylabel('y(t)')
13 title('Sample Sine Wave')
14 grid
這就是我們得到的:

當(dāng)我們對這條曲線fft時,我們希望在頻域得到以下頻譜(基于傅里葉變換理論,我們希望看見一個幅值為1的峰值在-4Hz處,另一個在+4Hz處)

使用FFT命令
我們知道目標(biāo)是什么了,那么現(xiàn)在使用Matlab的內(nèi)建的FFT函數(shù)來重新生成頻譜
1 %plot the frequency spectrum using the MATLAB fft command2 matlabFFT = figure; %create a new figure
3 YfreqDomain = fft(y); %take the fft of our sin wave, y(t)
4
5 stem(abs(YfreqDomain)); %use abs command to get the magnitude
6 %similary, we would use angle command to get the phase plot!
7 %we'll discuss phase in another post though!
8
9 xlabel('Sample Number')
10 ylabel('Amplitude')
11 title('Using the Matlab fft command')
12 grid
13 axis([0,100,0,120])
效果如下:
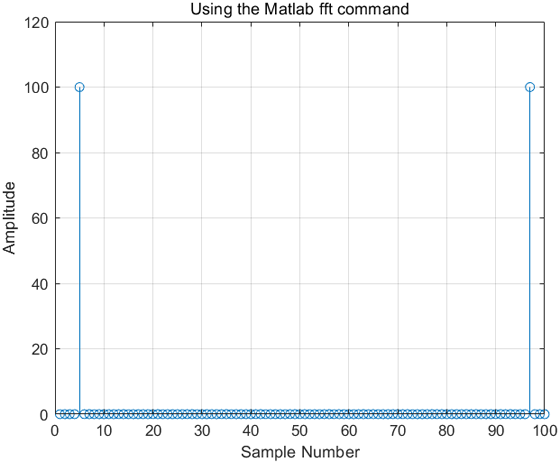
但是注意一下,這并不是我們真正想要的,有一些信息是缺失的
· x軸本來應(yīng)該給我們提供頻率信息,但是你能讀出頻率嗎?· 幅度都是100
· 沒有讓頻譜中心為0
為FFT定義一個函數(shù)來獲取雙邊頻譜
以下代碼可以簡化獲取雙邊頻譜的過程,復(fù)制并保存到你的.m文件中
1 function [X,freq]=centeredFFT(x,Fs)2 %this is a custom function that helps in plotting the two-sided spectrum
3 %x is the signal that is to be transformed
4 %Fs is the sampling rate
5
6 N=length(x);
7
8 %this part of the code generates that frequency axis
9 if mod(N,2)==0
10 k=-N/2:N/2-1; % N even
11 else
12 k=-(N-1)/2:(N-1)/2; % N odd
13 end
14 T=N/Fs;
15 freq=k/T; %the frequency axis
16
17 %takes the fft of the signal, and adjusts the amplitude accordingly
18 X=fft(x)/N; % normalize the data
19 X=fftshift(X); %shifts the fft data so that it is centered
這個函數(shù)輸出正確的頻域范圍和變換后的信號,它需要輸入需要變換的信號和采樣率。
接下來使用前文的正弦信號做一個簡單的示例,注意你的示例.m文件要和centeredFFT.m文件在一個目錄下
1 [YfreqDomain,frequencyRange] = centeredFFT(y,Fs);2 centeredFFT = figure;
3
4 %remember to take the abs of YfreqDomain to get the magnitude!
5 stem(frequencyRange,abs(YfreqDomain));
6 xlabel('Freq (Hz)')
7 ylabel('Amplitude')
8 title('Using the centeredFFT function')
9 grid
10 axis([-6,6,0,1.5])
效果如下:
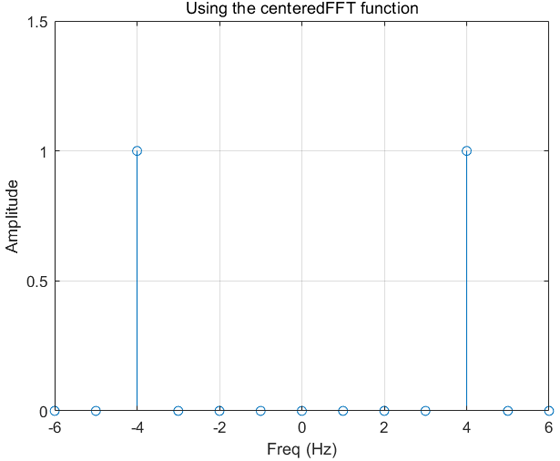
這張圖就滿足了我們的需求,我們得到了在+4和-4處的峰值,而且幅值為1.
為FFT定義一個函數(shù)來獲取右邊頻譜
從上圖可以看出,F(xiàn)FT變換得到的頻譜是左右對稱的,因此,我們只需要其中一邊就能獲得信號的所有信息,我們一般保留正頻率一側(cè)。
以下的函數(shù)對上面的自定義函數(shù)做了一些修改,讓它可以幫助我們只畫出信號的正頻率一側(cè)
1 function [X,freq]=positiveFFT(x,Fs)2 N=length(x); %get the number of points
3 k=0:N-1; %create a vector from 0 to N-1
4 T=N/Fs; %get the frequency interval
5 freq=k/T; %create the frequency range
6 X=fft(x)/N; % normalize the data
7
8 %only want the first half of the FFT, since it is redundant
9 cutOff = ceil(N/2);
10
11 %take only the first half of the spectrum
12 X = X(1:cutOff);
13 freq = freq(1:cutOff);
和前面一樣,使用正弦信號做一個示例,下面是示例代碼
1 [YfreqDomain,frequencyRange] = positiveFFT(y,Fs);2 positiveFFT = figure;
3 stem(frequencyRange,abs(YfreqDomain));
4 set(positiveFFT,'Position',[500,500,500,300])
5 xlabel('Freq (Hz)')
6 ylabel('Amplitude')
7 title('Using the positiveFFT function')
8 grid
9 axis([0,20,0,1.5])
效果如下:
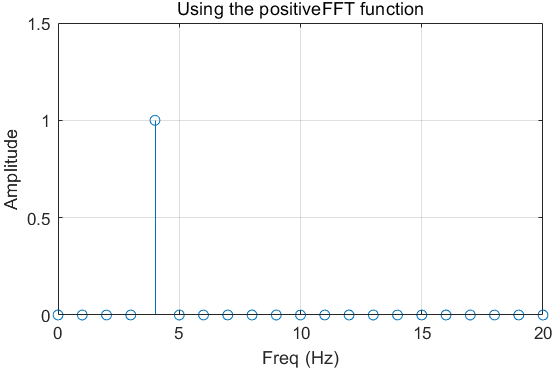

 粵公網(wǎng)安備 44030902003195號
粵公網(wǎng)安備 44030902003195號