歐拉公式是數學里最令人著迷的公式之一,它將數學里最重要的幾個常數聯系到了一起:兩個超越數:自然對數的底e,圓周率π;兩個單位:虛數單位i和自然數的單位1,以及數學里常見的0。

?而且它對數學領的締造也產生了廣泛影響,如三角函數、傅里葉級數、泰勒級數、概率論、群論等都有她的倩影。因此,數學家們評價它是“上帝創造的公式,我們只能看它卻不能完全理解它”。
?而且,這個公式對物理學影響也非常巨大,如機械波論、電磁學、波動光學、量子力學等匍匐在她的腳下;難怪物理學家查德·費曼驚呼:歐拉恒等式不但是“數學最奇妙的公式”,也是現代物理學的定量之跟,因為她把最基本的5個數學常數簡潔地連系起來,而且也將物理學中的圓周運動、簡諧振動、機械波、電磁波、概率波等聯系在了一起......
?歐拉恒等式是:
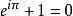
?其中e是自然指數的底,i是虛數單位,π是圓周率。這條恒等式第一次出現于1748年歐拉在洛桑出版的書Introduction,它是復分析的歐拉公式特例。對于任意實數x,則有
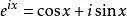
令x=π代入上式,則可得出歐拉恒等式。在歐拉公式中,虛數i占有特殊的地位,認識這個公式就需先從i開始:虛數i大家在高中接觸過,但那時我們只知道它是-1的平方根,可是它真正的意義是什么呢?這里有一條數軸,在數軸上有一個紅色線段,它的長度是1。當它乘以3的時候,它的長度發生了變化,變成了藍色的線段3,而當它乘以-1的時候,就變成了綠色的線段,或者說線段在數軸上圍繞原點旋轉了180度。
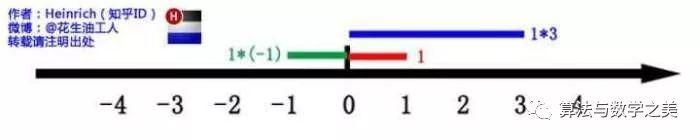
?我們知道乘-1其實就等于乘了兩次 i,因i×i=-1,這樣就使線段旋轉了180度,那么乘一次 i 呢?答案很簡單:旋轉了90度唄。
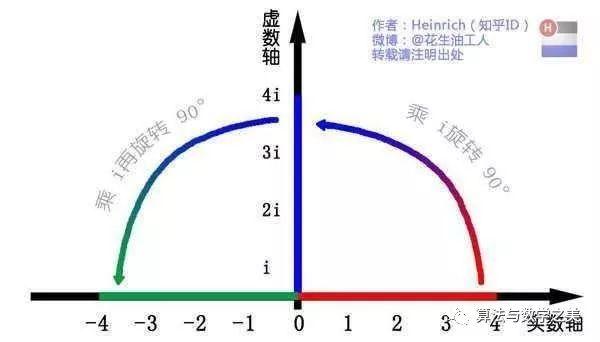
?如果我們將這種運算放到坐標平面上來表示,則實軸與虛軸就構成了一組對稱線段,我們再在0處安插一個垂直此線段的軸,這樣就構成了一個平面,我們稱之為復數平面;在這個平面上,我們可以看出,虛數i的功能就是旋轉。
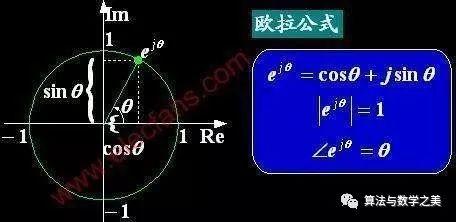
?對于歐拉公式
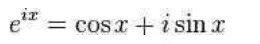
?這個公式在數學領域的意義要遠大于傅里葉分析,當x=π時,則有
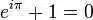
?它對描述圓周運動的物理意義就是圓心位移為0,如下圖:

?這個公式的關鍵作用就是將正弦波統一成了簡單的指數形式,我們來看看它圖像上的涵義:
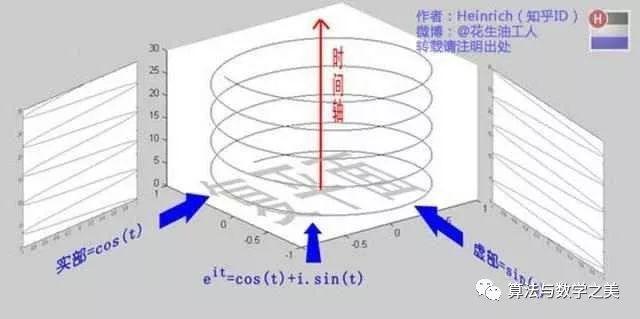
?可見,歐拉公式所描繪的正是在復平面上做圓周運動的點,隨著時間的改變,這個點在時間軸上就成了一條螺旋線。如果只看它的實數部分,也就是螺旋線在左側的投影,就是一個最基礎的余弦函數,而右側投影則是一個正弦函數。

?現代物理學告訴我們,宏觀宇宙的構成本質是旋轉的,帶有圓周運動和自旋性;微觀世界也是旋轉的,也帶有圓周運動和自旋性,而歐拉公式描述的核心正是旋轉與頻率,因此,在物理學定量意義上講,稱它是宇宙第一公式一點也不為過!

 粵公網安備 44030902003195號
粵公網安備 44030902003195號