麥克斯韋方程組

關(guān)于熱力學(xué)的方程，詳見“麥克斯韋關(guān)系式”。

麥克斯韋方程組（英語(yǔ)：Maxwell's equations）是英國(guó)物理學(xué)家麥克斯韋在19世紀(jì)建立的描述電磁場(chǎng)的基本方程組。

它含有四個(gè)方程，不僅分別描述了電場(chǎng)和磁場(chǎng)的行為，也描述了它們之間的關(guān)系。

麥克斯韋方程組是英國(guó)物理學(xué)家麥克斯韋在19世紀(jì)建立的描述電場(chǎng)與磁場(chǎng)的四個(gè)基本方程。

在麥克斯韋方程組中，電場(chǎng)和磁場(chǎng)已經(jīng)成為一個(gè)不可分割的整體。

該方程組系統(tǒng)而完整地概括了電磁場(chǎng)的基本規(guī)律，并預(yù)言了電磁波的存在。 　　

麥克斯韋提出的渦旋電場(chǎng)和位移電流假說的核心思想是：

變化的磁場(chǎng)可以激發(fā)渦旋電場(chǎng)，

變化的電場(chǎng)可以激發(fā)渦旋磁場(chǎng)；

電場(chǎng)和磁場(chǎng)不是彼此孤立的，

它們相互聯(lián)系、相互激發(fā)組成一個(gè)統(tǒng)一的電磁場(chǎng)

（也是電磁波的形成原理）。

麥克斯韋進(jìn)一步將電場(chǎng)和磁場(chǎng)的所有規(guī)律綜合起來，

建立了完整的電磁場(chǎng)理論體系。

這個(gè)電磁場(chǎng)理論體系的核心就是麥克斯韋方程組。 　　

麥克斯韋方程組，是英國(guó)物理學(xué)家詹姆斯·麥克斯韋在19世紀(jì)建立的一組描述電場(chǎng)、磁場(chǎng)與電荷密度、電流密度之間關(guān)系的偏微分方程。

從麥克斯韋方程組，可以推論出光波是電磁波。

麥克斯韋方程組和洛倫茲力方程是經(jīng)典電磁學(xué)的基礎(chǔ)方程。

從這些基礎(chǔ)方程的相關(guān)理論，發(fā)展出現(xiàn)代的電力科技與電子科技。 　　

麥克斯韋1865年提出的最初形式的方程組由20個(gè)等式和20個(gè)變量組成。

他在1873年嘗試用四元數(shù)來表達(dá)，但未成功。

現(xiàn)在所使用的數(shù)學(xué)形式是奧利弗·赫維賽德和約西亞·吉布斯于1884年以矢量分析的形式重新表達(dá)的。

麥克斯韋方程組的地位

麥克斯韋方程組在電磁學(xué)中的地位，如同牛頓運(yùn)動(dòng)定律在力學(xué)中的地位一樣。

以麥克斯韋方程組為核心的電磁理論，是經(jīng)典物理學(xué)最引以自豪的成就之一。

它所揭示出的電磁相互作用的完美統(tǒng)一，為物理學(xué)家樹立了這樣一種信念：

物質(zhì)的各種相互作用在更高層次上應(yīng)該是統(tǒng)一的。

另外，這個(gè)理論被廣泛地應(yīng)用到技術(shù)領(lǐng)域。

1845年，關(guān)于電磁現(xiàn)象的三個(gè)最基本的實(shí)驗(yàn)定律：

庫(kù)侖定律（1785年），

安培—畢奧—薩伐爾定律（1820年），

法拉第定律（1831-1845年）已被總結(jié)出來，

法拉第的“電力線”和“磁力線”概念已發(fā)展成“電磁場(chǎng)概念”。

場(chǎng)概念的產(chǎn)生，也有麥克斯韋的一份功勞，這是當(dāng)時(shí)物理學(xué)中一個(gè)偉大的創(chuàng)舉，因?yàn)檎菆?chǎng)概念的出現(xiàn)，使當(dāng)時(shí)許多物理學(xué)家得以從牛頓“超距觀念”的束縛中擺脫出來，普遍地接受了電磁作用和引力作用都是“近距作用”的思想。　　

1855年至1865年，麥克斯韋在全面地審視了庫(kù)侖定律、安培—畢奧—薩伐爾定律和法拉第定律的基礎(chǔ)上，把數(shù)學(xué)分析方法帶進(jìn)了電磁學(xué)的研究領(lǐng)域，由此導(dǎo)致麥克斯韋電磁理論的誕生。

麥克斯韋方程組的積分形式:

（1）描述了電場(chǎng)的性質(zhì)。

電荷是如何產(chǎn)生電場(chǎng)的高斯定理。

（靜電場(chǎng)的高斯定理）

電場(chǎng)強(qiáng)度在一封閉曲面上的面積分與封閉曲面所包圍的電荷量成正比。

電場(chǎng)E （矢量）通過任一閉曲面的通量，即對(duì)該曲面的積分等于4π乘以該曲面所包圍的總電荷量。

靜電場(chǎng)（見電場(chǎng)）的基本方程之一，它給出了電場(chǎng)強(qiáng)度在任意封閉曲面上的面積分和包圍在封閉曲面內(nèi)的總電量之間的關(guān)系。

根據(jù)庫(kù)侖定律可以證明電場(chǎng)強(qiáng)度對(duì)任意封閉曲面的通量正比于該封閉曲面內(nèi)電荷的代數(shù)和，

通過任意閉合曲面的電通量等于該閉合曲面所包圍的所有電荷量的代數(shù)和與電常數(shù)之比。

電場(chǎng)強(qiáng)度對(duì)任意封閉曲面的通量只取決于該封閉曲面內(nèi)電荷的代數(shù)和，與曲面內(nèi)電荷的分布情況無(wú)關(guān)，與封閉曲面外的電荷亦無(wú)關(guān)。

在真空的情況下,Σq是包圍在封閉曲面內(nèi)的自由電荷的代數(shù)和。

當(dāng)存在介質(zhì)時(shí),Σq應(yīng)理解為包圍在封閉曲面內(nèi)的自由電荷和極化電荷的總和。

在靜電場(chǎng)中，由于自然界中存在著獨(dú)立的電荷，所以電場(chǎng)線有起點(diǎn)和終點(diǎn)，只要閉合面內(nèi)有凈余的正（或負(fù)）電荷，穿過閉合面的電通量就不等于零，即靜電場(chǎng)是有源場(chǎng)；

高斯定理反映了靜電場(chǎng)是有源場(chǎng)這一特性。

凡是有正電荷的地方，必有電力線發(fā)出；凡是有負(fù)電荷的地方，必有電力線會(huì)聚。

正電荷是電力線的源頭，負(fù)電荷是電力線的尾閭。

高斯定理是從庫(kù)侖定律直接導(dǎo)出的，它完全依賴于電荷間作用力的二次方反比律。

把高斯定理應(yīng)用于處在靜電平衡條件下的金屬導(dǎo)體，就得到導(dǎo)體內(nèi)部無(wú)凈電荷的結(jié)論，因而測(cè)定導(dǎo)體內(nèi)部是否有凈電荷是檢驗(yàn)庫(kù)侖定律的重要方法。

對(duì)于某些對(duì)稱分布的電場(chǎng),如均勻帶電球的電場(chǎng),無(wú)限大均勻帶電面的電場(chǎng)以及無(wú)限長(zhǎng)均勻帶電圓柱的電場(chǎng)，可直接用高斯定理計(jì)算它們的電場(chǎng)強(qiáng)度。

電位移對(duì)任一面積的能量為電通量，因而電位移亦稱電通密度。

（2）描述了變化的磁場(chǎng)激發(fā)電場(chǎng)的規(guī)律。 　　

磁場(chǎng)是如何產(chǎn)生電場(chǎng)的法拉第電磁感應(yīng)定律。

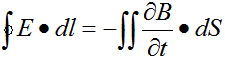（靜電場(chǎng)的環(huán)路定理）

在沒有自由電荷的空間，由變化磁場(chǎng)激發(fā)的渦旋電場(chǎng)的電場(chǎng)線是一系列的閉合曲線。

在一般情況下，電場(chǎng)可以是庫(kù)侖電場(chǎng)也可以是變化磁場(chǎng)激發(fā)的感應(yīng)電場(chǎng)，而感應(yīng)電場(chǎng)是渦旋場(chǎng)，它的電位移線是閉合的，對(duì)封閉曲面的通量無(wú)貢獻(xiàn)。　　

麥克斯韋提出的渦旋電場(chǎng)的概念，揭示出變化的磁場(chǎng)可以在空間激發(fā)電場(chǎng)，并通過法拉第電磁感應(yīng)定律得出了二者的關(guān)系，上式表明，任何隨時(shí)間而變化的磁場(chǎng)，都是和渦旋電場(chǎng)聯(lián)系在一起的。

（3）描述了磁場(chǎng)的性質(zhì)。

論述了磁單極子的不存在的高斯磁定律　

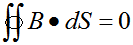（穩(wěn)恒磁場(chǎng)的高斯定理）

在磁場(chǎng)中，由于自然界中沒有單獨(dú)的磁極存在，N極和S極是不能分離的，磁感線都是無(wú)頭無(wú)尾的閉合線，所以通過任何閉合面的磁通量必等于零。

由于磁力線總是閉合曲線，因此任何一條進(jìn)入一個(gè)閉合曲面的磁力線必定會(huì)從曲面內(nèi)部出來，否則這條磁力線就不會(huì)閉合起來了。如果對(duì)于一個(gè)閉合曲面，定義向外為正法線的指向，則進(jìn)入曲面的磁通量為負(fù)，出來的磁通量為正，那么就可以得到通過一個(gè)閉合曲面的總磁通量為0。

這個(gè)規(guī)律類似于電場(chǎng)中的高斯定理，因此也稱為高斯定理。

（4）描述了變化的電場(chǎng)激發(fā)磁場(chǎng)的規(guī)律。 　　

電流和變化的電場(chǎng)是怎樣產(chǎn)生磁場(chǎng)的麥克斯韋-安培定律。

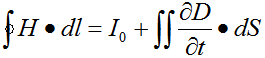（磁場(chǎng)的安培環(huán)路定理）

變化的電場(chǎng)產(chǎn)生的磁場(chǎng)和傳導(dǎo)電流產(chǎn)生的磁場(chǎng)相同，都是渦旋狀的場(chǎng)，磁感線是閉合線。因此，磁場(chǎng)的高斯定理仍適用。

在穩(wěn)恒磁場(chǎng)中，磁感強(qiáng)度H沿任何閉合路徑的線積分，等于這閉合路徑所包圍的各個(gè)電流之代數(shù)和。

磁場(chǎng)可以由傳導(dǎo)電流激發(fā)，也可以由變化電場(chǎng)的位移電流所激發(fā)，它們的磁場(chǎng)都是渦旋場(chǎng)，磁感應(yīng)線都是閉合線，對(duì)封閉曲面的通量無(wú)貢獻(xiàn)。　

麥克斯韋提出的位移電流的概念，揭示出變化的電場(chǎng)可以在空間激發(fā)磁場(chǎng)，并通過全電流概念的引入，得到了一般形式下的安培環(huán)路定理在真空或介質(zhì)中的表示形式，上式表明，任何隨時(shí)間而變化的電場(chǎng)，都是和磁場(chǎng)聯(lián)系在一起的。

合體：

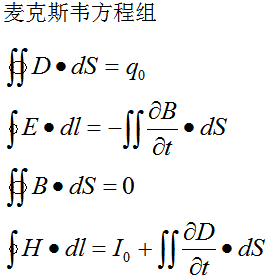
式中H為磁場(chǎng)強(qiáng)度,D為電通量密度,E為電場(chǎng)強(qiáng)度，B為磁通密度。

在采用其他單位制時(shí),方程中有些項(xiàng)將出現(xiàn)一常數(shù)因子,如光速c等。

上面四個(gè)方程組成：

描述電荷如何產(chǎn)生電場(chǎng)的高斯定律、

描述時(shí)變磁場(chǎng)如何產(chǎn)生電場(chǎng)的法拉第感應(yīng)定律、

論述磁單極子不存在的高斯磁定律、

描述電流和時(shí)變電場(chǎng)怎樣產(chǎn)生磁場(chǎng)的麥克斯韋-安培定律。

綜合上述可知，變化的電場(chǎng)和變化的磁場(chǎng)彼此不是孤立的，它們永遠(yuǎn)密切地聯(lián)系在一起，相互激發(fā)，組成一個(gè)統(tǒng)一的電磁場(chǎng)的整體。

這就是麥克斯韋電磁場(chǎng)理論的基本概念。

麥克斯韋方程組的積分形式反映了空間某區(qū)域的電磁場(chǎng)量(D、E、B、H)和場(chǎng)源(電荷q、電流I)之間的關(guān)系。

麥克斯韋方程組微分形式：

式中J為電流密度,，ρ為電荷密度。

H為磁場(chǎng)強(qiáng)度,D為電通量密度,E為電場(chǎng)強(qiáng)度，B為磁通密度。

上圖分別表示為：

（1）磁場(chǎng)強(qiáng)度的旋度（全電流定律）等于該點(diǎn)處傳導(dǎo)電流密度 與位移電流密度 的矢量和；
（2）電場(chǎng)強(qiáng)度的旋度（法拉第電磁感應(yīng)定律）等于該點(diǎn)處磁感強(qiáng)度變化率的負(fù)值；
（3）磁感強(qiáng)度的散度處處等于零 （磁通連續(xù)性原理） 。
（4）電位移的散度等于該點(diǎn)處自由電荷的體密度 （高斯定理） 。

在電磁場(chǎng)的實(shí)際應(yīng)用中，經(jīng)常要知道空間逐點(diǎn)的電磁場(chǎng)量和電荷、電流之間的關(guān)系。

從數(shù)學(xué)形式上，就是將麥克斯韋方程組的積分形式化為微分形式。

上面的微分形式分別表示：

（1）電位移的散度等于該點(diǎn)處自由電荷的體密度 （高斯定理） 。
（2）磁感強(qiáng)度的散度處處等于零 （磁通連續(xù)性原理） 。
（3）電場(chǎng)強(qiáng)度的旋度（法拉第電磁感應(yīng)定律）等于該點(diǎn)處磁感強(qiáng)度變化率的負(fù)值；
（4）磁場(chǎng)強(qiáng)度的旋度（全電流定律）等于該點(diǎn)處傳導(dǎo)電流密度 與位移電流密度 的矢量和；

利用矢量分析方法，可得：

(1)在不同的慣性參照系中，麥克斯韋方程有同樣的形式。 　　
(2) 應(yīng)用麥克斯韋方程組解決實(shí)際問題，還要考慮介質(zhì)對(duì)電磁場(chǎng)的影響。
例如在各向同性介質(zhì)中，電磁場(chǎng)量與介質(zhì)特性量有下列關(guān)系： 
在非均勻介質(zhì)中，還要考慮電磁場(chǎng)量在界面上的邊值關(guān)系。
在利用t=0時(shí)場(chǎng)量的初值條件，原則上可以求出任一時(shí)刻空間任一點(diǎn)的電磁場(chǎng)，即E(x,y,z,t)和B(x,y,z,t)。 

科學(xué)意義

經(jīng)典場(chǎng)論是19世紀(jì)后期麥克斯韋在總結(jié)電磁學(xué)三大實(shí)驗(yàn)定律，并把它與力學(xué)模型進(jìn)行類比的基礎(chǔ)上創(chuàng)立起來的。

但麥克斯韋的主要功績(jī)恰恰是他能夠跳出經(jīng)典力學(xué)框架的束縛：

在物理上以"場(chǎng)"而不是以"力"作為基本的研究對(duì)象，在數(shù)學(xué)上引入了有別于經(jīng)典數(shù)學(xué)的矢量偏微分運(yùn)算符。

這兩條是發(fā)現(xiàn)電磁波方程的基礎(chǔ)。

這就是說，實(shí)際上麥克斯韋的工作已經(jīng)沖破經(jīng)典物理學(xué)和經(jīng)典數(shù)學(xué)的框架，只是由于當(dāng)時(shí)的歷史條件，人們?nèi)匀恢荒軓呐ｎD的經(jīng)典數(shù)學(xué)和力學(xué)的框架去理解電磁場(chǎng)理論。　　

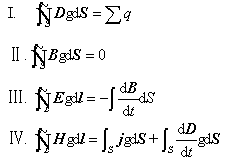
現(xiàn)代數(shù)學(xué)，Hilbert空間中的數(shù)學(xué)分析是在19世紀(jì)與20世紀(jì)之交的時(shí)候才出現(xiàn)的。

而量子力學(xué)的物質(zhì)波的概念則在更晚的時(shí)候才被發(fā)現(xiàn)，特別是對(duì)于現(xiàn)代數(shù)學(xué)與量子物理學(xué)之間的不可分割的數(shù)理邏輯聯(lián)系至今也還沒有完全被人們所理解和接受。

從麥克斯韋建立電磁場(chǎng)理論到現(xiàn)在，人們一直以歐氏空間中的經(jīng)典數(shù)學(xué)作為求解麥克斯韋方程組的基本方法。

我們從麥克斯韋方程組的產(chǎn)生,形式,內(nèi)容和它的歷史過程中可以看到：

第一，物理對(duì)象是在更深的層次上發(fā)展成為新的公理表達(dá)方式而被人類所掌握，所以科學(xué)的進(jìn)步不會(huì)是在既定的前提下演進(jìn)的，一種新的具有認(rèn)識(shí)意義的公理體系的建立才是科學(xué)理論進(jìn)步的標(biāo)志。

第二，物理對(duì)象與對(duì)它的表達(dá)方式雖然是不同的東西，但如果不依靠合適的表達(dá)方法就無(wú)法認(rèn)識(shí)到這個(gè)對(duì)象的"存在"。

第三，我們正在建立的理論將決定到我們?cè)诤畏N層次的意義上使我們的對(duì)象成為物理事實(shí),這正是現(xiàn)代最前沿的物理學(xué)所給我們帶來的困惑。

麥克斯韋方程組揭示了電場(chǎng)與磁場(chǎng)相互轉(zhuǎn)化中產(chǎn)生的對(duì)稱性優(yōu)美，這種優(yōu)美以現(xiàn)代數(shù)學(xué)形式得到充分的表達(dá)。

但是，我們一方面應(yīng)當(dāng)承認(rèn)，恰當(dāng)?shù)臄?shù)學(xué)形式才能充分展示經(jīng)驗(yàn)方法中看不到的整體性(電磁對(duì)稱性)，但另一方面，我們也不應(yīng)當(dāng)忘記，這種對(duì)稱性的優(yōu)美是以數(shù)學(xué)形式反映出來的電磁場(chǎng)的統(tǒng)一本質(zhì)。

因此我們應(yīng)當(dāng)認(rèn)識(shí)到應(yīng)在數(shù)學(xué)的表達(dá)方式中"發(fā)現(xiàn)"或"看出" 了這種對(duì)稱性，而不是從物理數(shù)學(xué)公式中直接推演出這種本質(zhì)。